差集め算を面積図を使って解く方法はすでにYouTubeなどでも解説されています。
しかし、その解説されている面積図を理解すること自体が難しかったりしますよね。そこで少しでも解きやすくなるよう、簡単に描けるやりかたを考えてみました。
差集め算の面積図の書き方
基本問題
問題①
まず、こんな図を書いてみましょう。
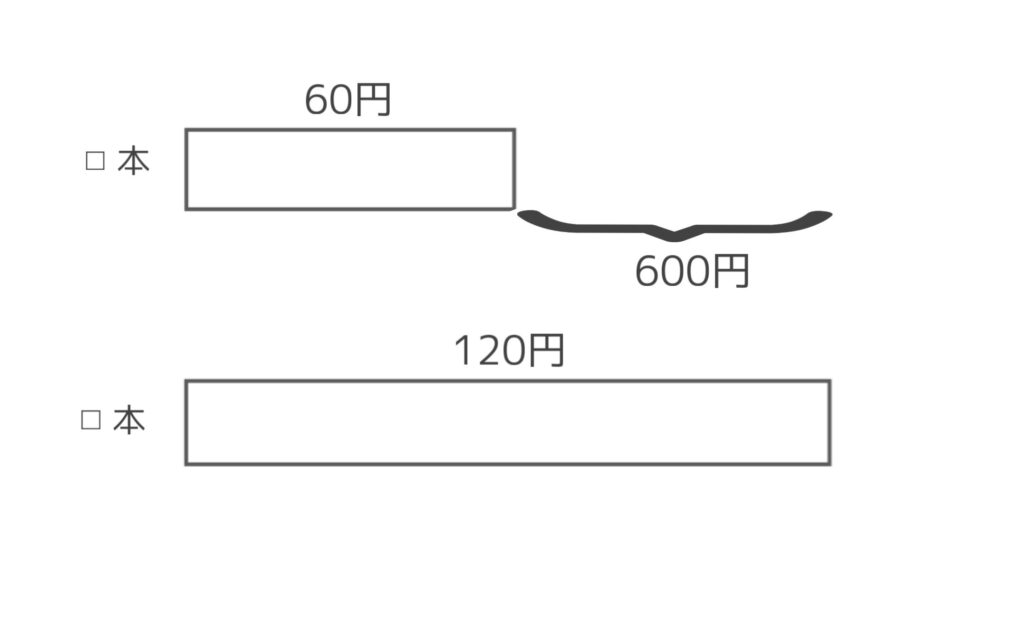
- 上の面積がえん筆の合計代金
- 下の面積がボールペンの合計代金
面積の縦は◻︎本、横が1本あたりの金額です。面積の差の部分は、全体の差となり600円です。
書き方の順序は次のとおり。
①問題文の「同じ本数ずつ」に着目し、面積の左側にえん筆とボールペンそれぞれの◻︎本と書きます。面積の縦棒も書きます。同じ数なので、それぞれ同じ長さであることが分かります。
②面積の横をそれぞれの一本あたりの金額とします。えん筆が60円でボールペン120円です。ボールペンは鉛筆の2倍の金額なので、だいたい倍の長さで横の長さを設定します。
こうしてそれぞれの面積を完成します。
③面積差の部分を図のようにして600円とします。全体の差をこう書いて理解しておきます。
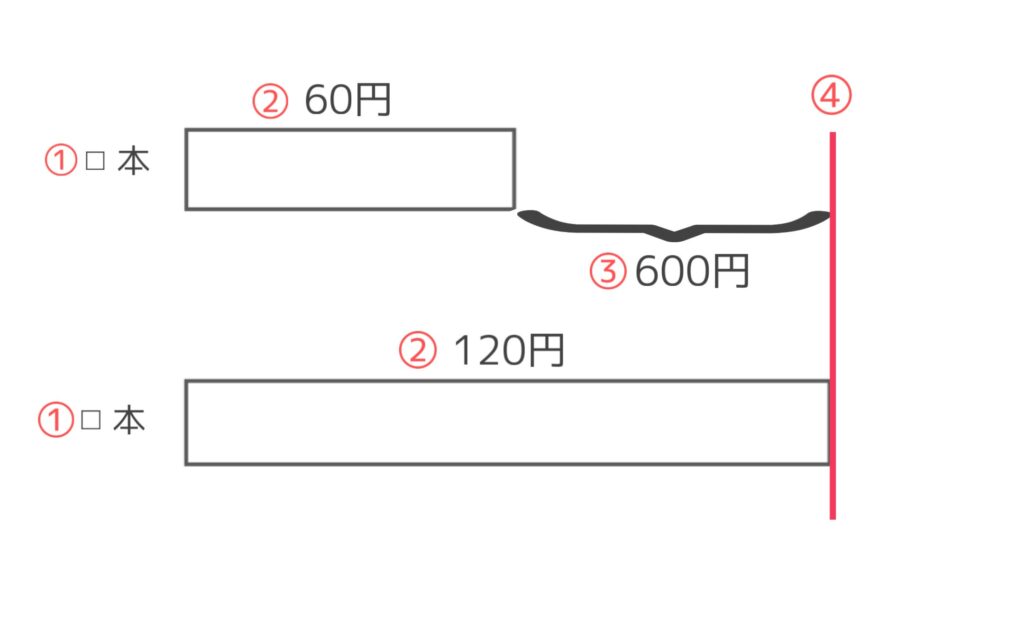
④面積図の右側の赤縦棒の部分も意識づけてください。難易度が上がれば上がるほど重要になります。600円の差が埋まれば、ボールペンの代金と同じだよねと把握しておきます。
差集め算の基本公式
全体の差➗一個あたりの差=個数
今回の全体の差は、代金差の600円。一個あたりの差は120円ー60円=60円。したがって、600➗60=10。10本ずつが正解となります。
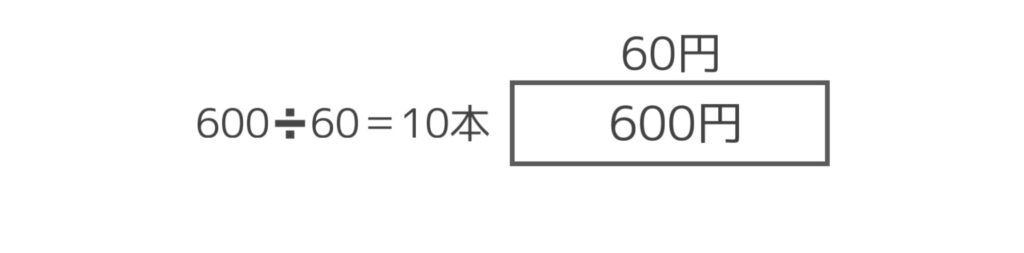
面積の公式に当てはめると◻︎✖️60=600。これを逆算して600➗60=10になるわけです。
初めの方の面積図で、面積差の表し方を『 }』を使って600円としている理由は、その方が大きい面積と小さい面積の差が見えやすいからです。
問題②
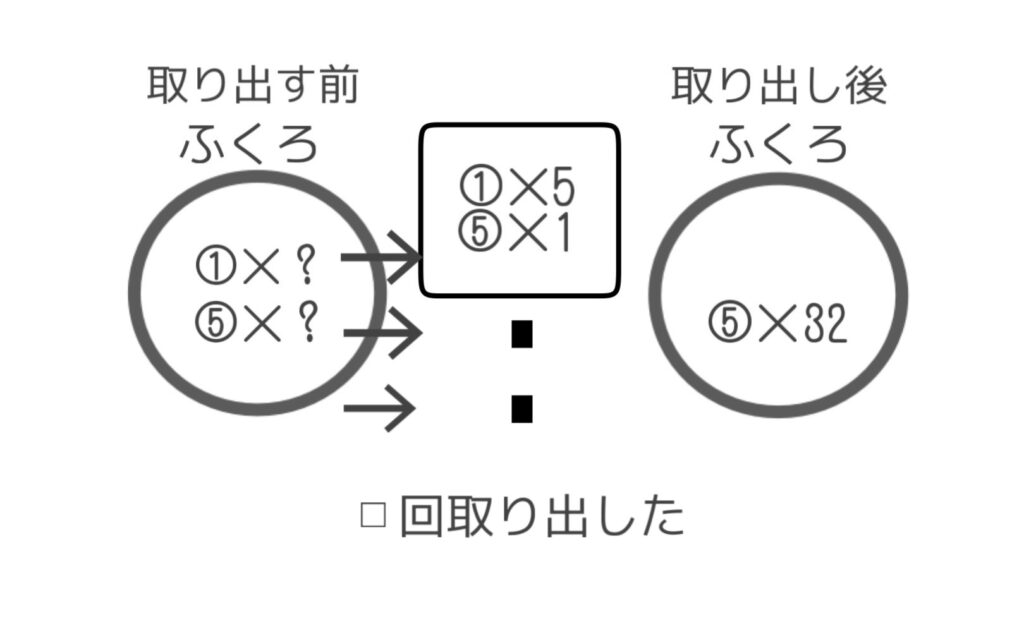
面積図を書く前段階として、問題文のイメージを描いてどういう状況なのかつかんでおくのも良いでしょう。
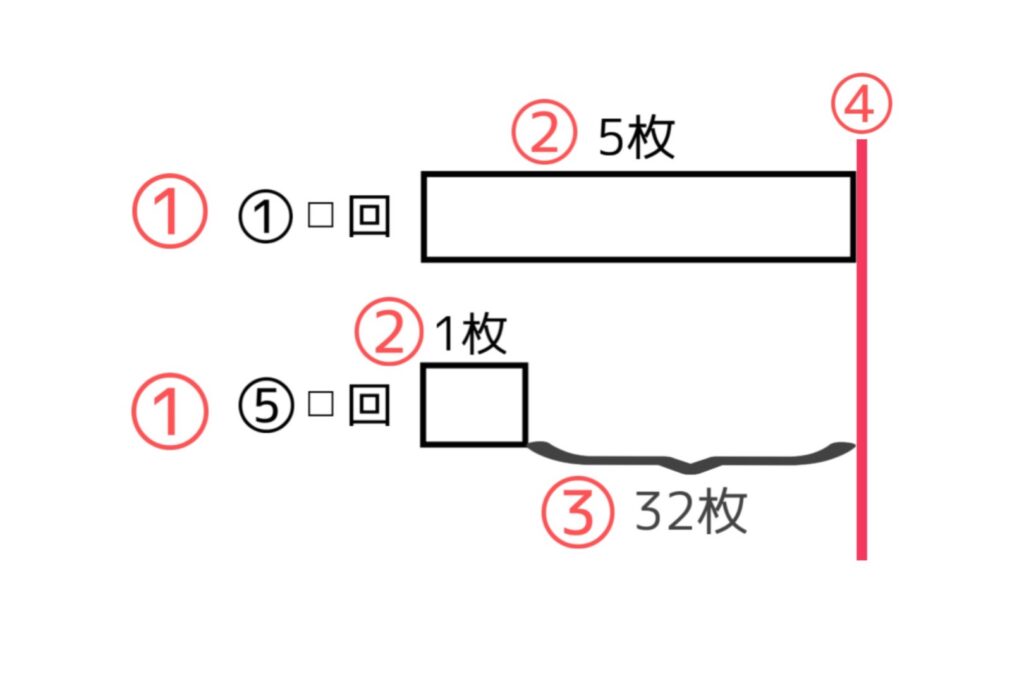
①問題文の「同時に」着目です。同時に何回か取り出したとあるので、この取り出した回数が面積の縦にくるのではないかと想像します。
②横は1回に取り出す枚数です。
③今回の全体の差は、32枚ですね。
④縦赤棒は5円玉をあと32枚取り出したら、1円玉の枚数と同じになるを表します。問題文より、すべての1円玉の枚数と5円玉の枚数は同じですからね。
全体の差32枚➗一回あたりの差4=8回
答えは8回でした。
この問題、いっけん複雑なようですが、面積図にするとかなり簡単であることが分かります。面積図は単に取り出した枚数差を表しているだけですね。
個数をそろえる系
youtubeなどで紹介されているやり方で2つの面積の縦横の長さがそれぞれ違うものがあります。これは個数をそろえずそのまま面積図を書くやり方です。
僕はあの面積図を見てもどうしても理解ができません。はみ出しているところが共通だよね!と言われても視覚的には分からないんですよね。涙
僕が考えた方法を使えば個数をそろえることを意識しなくても、自動的にそろいます。
問題①
問題文の「Aの方が5個多いですが」より、個数が違うことが分かります。この個数をそろえていく必要があります。
面積図の縦には個数がくるので、面積の縦の長さを変えたくなりますが、それはやりません。縦も横も違う面積ができて分かりにくいです。
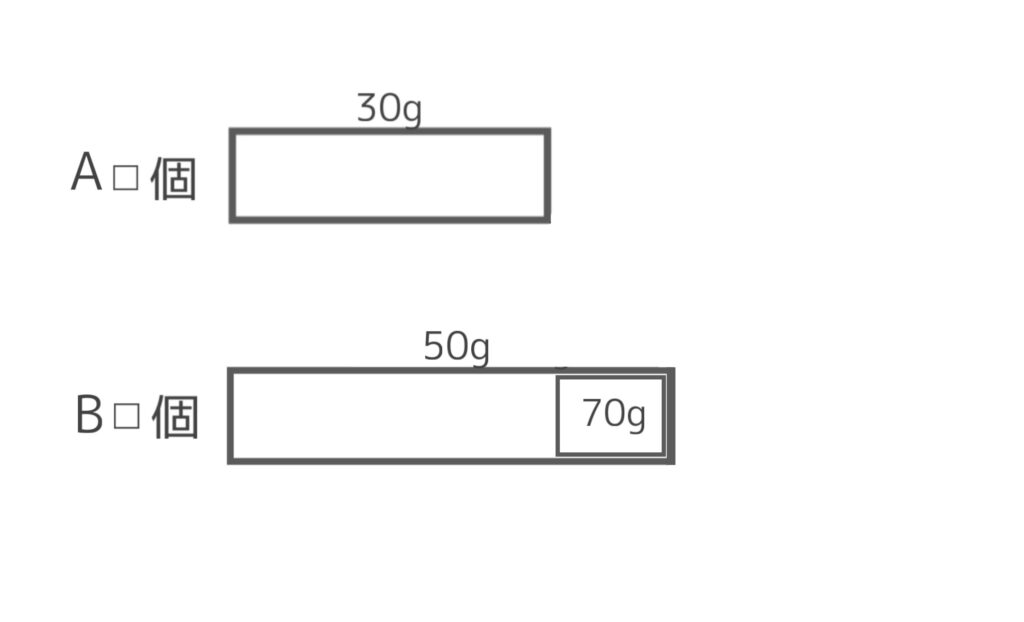
まず、縦の長さはそれぞれ同じにしといて、面積図を書き始めます。
Bのおもりの面積における70gは問題文の「Aの合計の重さより70g重い」のことです。
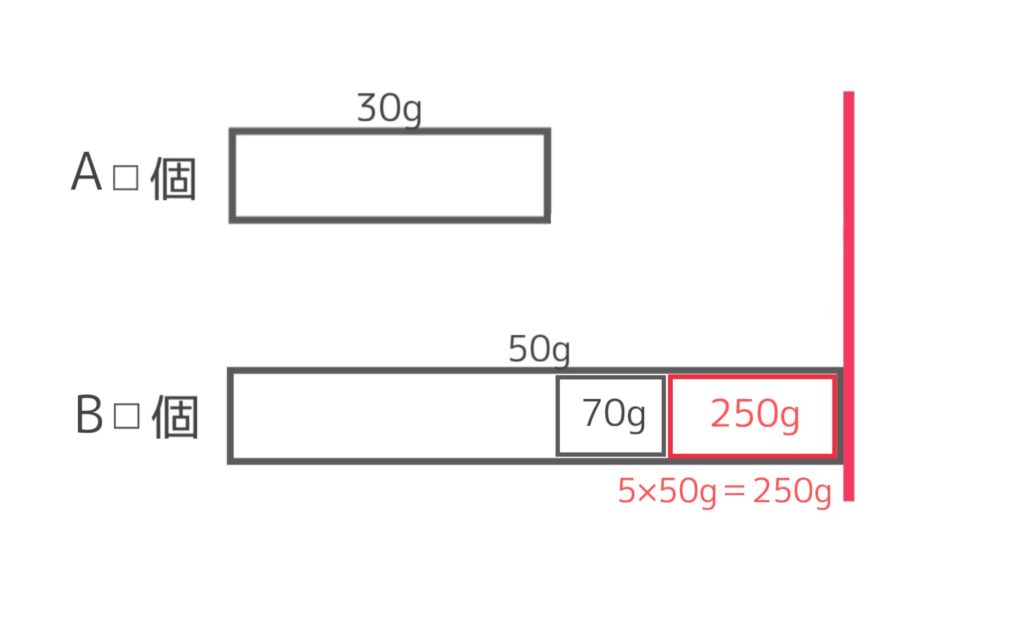
続いて、赤字の部分の250gは何かというと、Bの方におもりを5個分加えたイメージです。もともとAの方が5個多いので、Bの数を増やして個数をそろえた状態ですね。
個数をそろえるは、このように重さに換算したものを加えておくということです。だからそれぞれの面積の縦の長さは同じままなんですね。
Bの面積の横の長さは50gのままです。250g分の面積が加わって面積が横に伸びても、横幅の50gはそのままっていうのが何かしっくりこないかもしれません。でも、慣れていきましょう。
こうして、全体の差を求めることができました。
Aの面積とBの面積の差(全体の差)を出すと、
70g +250g=320g
一個あたりのg差は、
50gー30g=20g。
全体の差➗一個あたりのg差で面積の縦を求めるので、、
320➗20=16個
面積の縦の数はそれぞれ16個です。
よって、まずAのおもりが16個。
Bのおもりは仮に5個追加してましたから、16ー5で11個となります。
以上でした。
ちょっと、おもりが多すぎて、ある意味重い問題になっちゃいましたね笑
必ずしも使う必要はない
差集め算は面積図で考えると解きやすいとはいうものの、全ての問題に当てはめようとするとかえって難しくなります。
例えば、この問題。
この問題は線分図を使った方がいいです。
あくまでも面積図を使えば解きやすくなる場合がある、ということ。当てはまらなければ別で考えるということを念頭に置いておきましょう。



コメント