たいぽん式の差集め算の解き方は、まず面積図で解くことを考えます。そして、面積図を描こうとしてもどうもこれじゃあ分かりづらいぞとなった時に線分図を使います。
また、慣れてくると、この問題は面積図で描くよりか、線分図で描く方がいいなということが問題文を読んでいるうちにわかるようになってきます。
この回ではそういった、線分図系の問題を集めて解法を載せてみました。
線分図系の差集め算
問題①
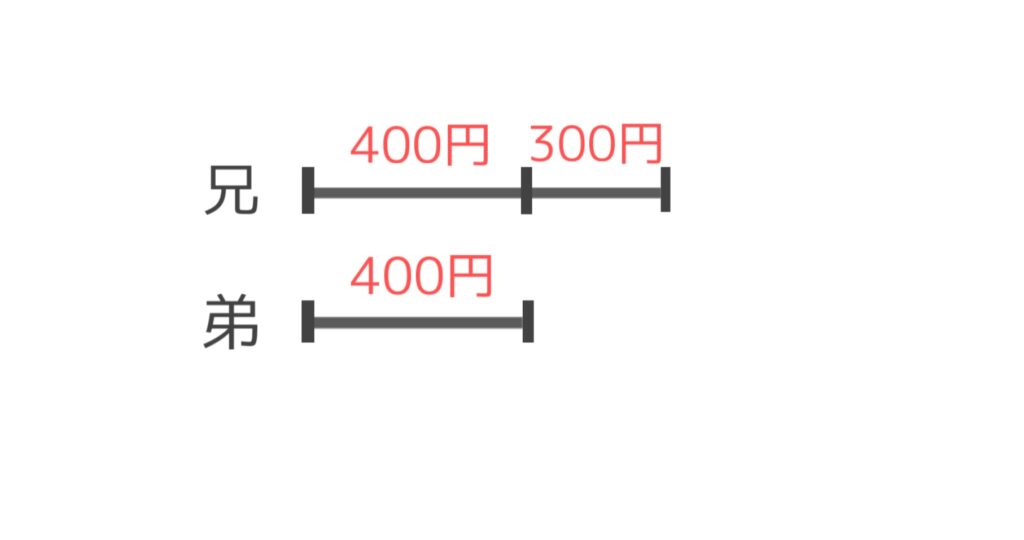
線分図を書くときは、このようにしていくら差があるか明らかにしておくことが重要です。兄の700円は、弟との共通部分の400円+差の300円が合わさってできています。
差をとるということは、何ヶ月貯金しても共通部分の400円は0円です(400円ー400円)。ということは、差の部分だけが積み重なっていくイメージですね。
2400円➗300円=8
答えは8ヶ月でした。
これは簡単な問題です。次の問題は少しむずいです。
問題②
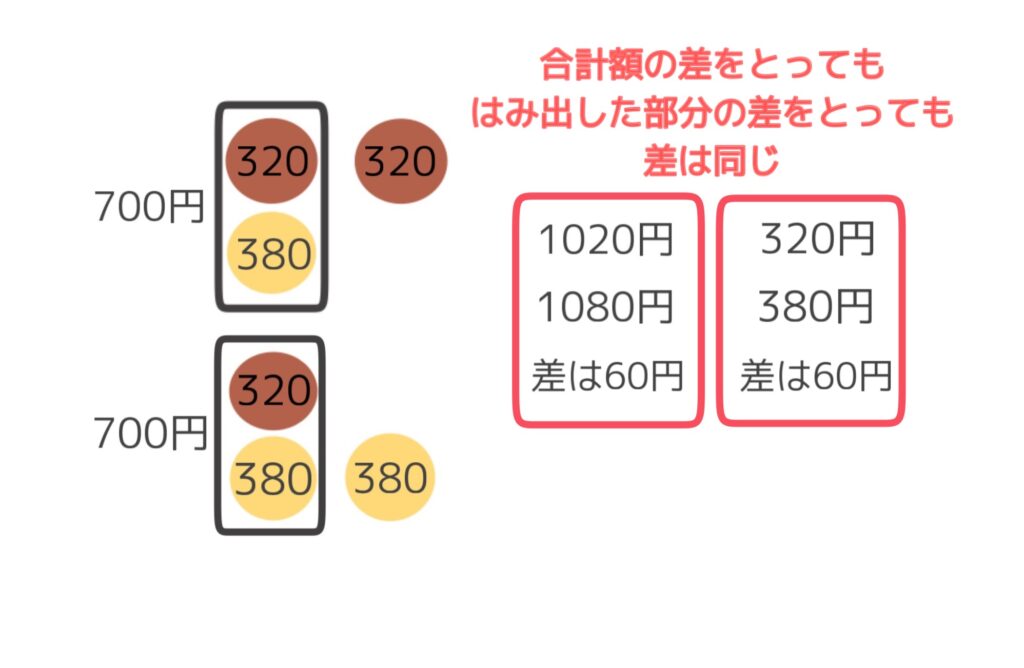
上図に書いてある通り、合計額の差をとっても、はみ出した部分の差をとっても差は同じです。
仲良く2個ずつある部分はそれぞれ700円なので、この部分の差は0円です。
ということは、この2個ずつの部分700円が左に1セット、2セットと増えていったとしても、仲良く並んでいる限り差は0円です。
これらのことを前提にあらためて問題に戻ってみます。
問題文「個数は3個ちがいます」より、ガトーショコラかモンブランのどちらかが3個はみだしていることになります。
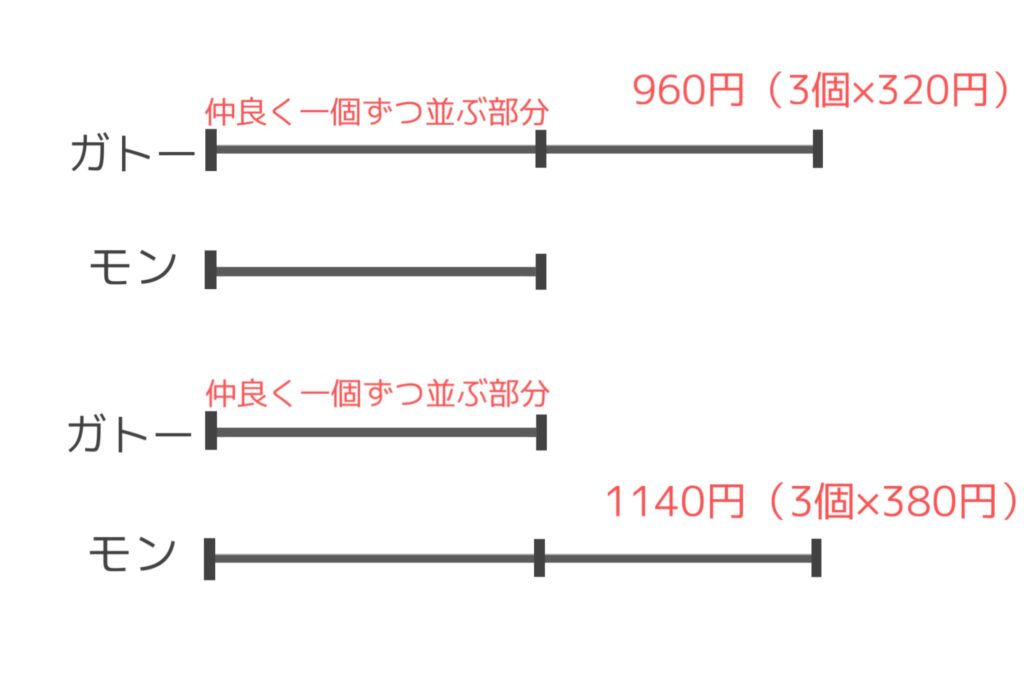
ということは、問題文の代金合計額3060円からはみ出している金額を引いてみると、残りは仲良く1個ずつ並んでいる部分が残ることになります。
ガトーショコラが3個多い場合は。
3060円ー960円(はみ出し部分)=2100円
2100円は仲良く並んでいる部分なのでガトーショコラとモンブラン1個ずつの1セットの700円で割り切れる必要があります。
2100円➗700円=3セット
割り切れました!
ということは、2100円の中にはガトーショコラとモンブランが3個ずつです。
この場合の全部の個数は、ガトーショコラが3+3で6個。モンブランが3個です。
もう一方の方をやってみましょう。
同じように代金合計額3060円から、モンブランのはみしだし部分の金額1140円を引きます。
3060円ー1140円=1920円
1920円は仲良く並んでいる部分なのでガトーショコラとモンブラン1個ずつの1セットの700円で割り切れる必要があります。
1920円➗700円=2.744…
割り切れません。
1個ずつ仲良く入っているはずなので、ガトーショコラとモンブラン1個ずつの1セット700円で割り切れるはずですよね。でも割り切れません。
したがって、答えは前の方が正解となります。
ガトーショコラ6個、モンブラン3個が正解です。
まとめ
実際にテストなどで、問題が出されてくると、面積図でやった方が良いか、線分図でやった方が良いか問題文を読んで判断しなければなりません。
その時の順序はまず、面積図で描けないか考える。やりづらいなら、線分図で考えるようにしましょう。
かなり慣れてくると上記のような問題を見て初めから線分図を使えるようになれます。



コメント